Patrick Meaney
Web App Software Engineer
- Portfolio
- Background
- Services

Predictive & Descriptive Statistical Analysis
Predicting rates of crime based on economic indicators (R — statistical computing)
As part of my graduate statistics course "Advanced Statistical Methods", using R, I data-engineered a dataset from public datasets, then tested various predictive models for their accuracy.
After finding the right model, I demonstrate a training model and test real data against it. Similar methodology, on a larger scale, could be replicated to make predictions of business outcomes. (In fact, one project I would like to work on is a D3 web dashboard for business metrics statistically derived with R or Python).
Here is the model I settled on: (note: each datapoint is per zipcode)
[Crime] per capita prediction = [% of Population Below Poverty Level] _ [Median Household Income] _ [Median Rent price]
(Where Crime = Assault, Robbery, Burglary, or Theft, and * = interaction effects)
Trained Models
Here are three examples of trained models tested with actual data. It's a multivariate linear regression model trained with 80% of the dataset, and tested with 20%. Each time I test the model, a new randomly selected training model is created.
Test 1 of Assault, Robbery, Burglary and Theft models

Test 2 of Assault, Robbery, Burglary and Theft models

Test 3 of Assault, Robbery, Burglary and Theft models

The Explanation: How does this project work?
The project is a Multilinear regression model which seeks to determine:
"To what degree can a neighborhood's (i.e. zipzcode's) crime rates be predicted with the following economic factors?" (which is what this summary represents).
- Zipcode-based Economic factor 1: % of Population Below Poverty Level
- Zipcode-based Economic factor 2: Median Household Income
- Zipcode-based Economic factor 3: Median Rent price of dwellings
The anwser is YES, quite strongly-- with 70-80% confidence, depending on crime type, in Austin, TX
I aggregated data from, and data-engineered, the following datasets:
- 2014 Housing Market Analysis Dataset (Government Open Data initiative for Austin, TX): Source of % of Population Below Poverty Level, Median Household Income, Median Rent price
- 2014 Crime dataset (Government Open Data initiative for Austin, TX): 40,000 rows -- I aggregated & simplified variations of crime names using regex
- 2012 US Population Per Zipcode dataset: R's local data library to access 2012 population statistics, using the following command: data(df_pop_zip)
- 2015 U.S. Gazetteer Map Data / US Census Department Geographic dataset: Although I aggregated this data into the final data table, it did not go into the final model
Data table
After doing some data hygiene & data engineering (such as to assimilate similar categories-- e.g. different types of theft) the result is cleansed data, aggregated into following table.
The result is cleansed data, aggregated into following table.
Data table used in the model. Scroll Horizontally & Vertically to see all data
| # | zipcode | SqMtrs | SqKm | PopulationBelowPovertyLevel | MedianHouseholdIncome | Unemployment | MedianRent | population | assault | burglary | homicide | rape | robbery | theft | assault_perCapita | burglary_perCapita | homicide_perCapita | rape_perCapita | robbery_perCapita | theft_perCapita | totalCrimes | totalCrimesPerCapita |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 78617 | 179810277 | 179.810277 | 18 | 43957 | 15 | 1041 | 19553 | 14 | 48 | 0 | 10 | 12 | 190 | 0.000716002659438449 | 0.00245486626093183 | 0 | 0.000511430471027464 | 0.000613716565232957 | 0.00971717894952181 | 274 | 0.0140131949061525 |
| 2 | 78701 | 4218139 | 4.218139 | 20 | 68152 | 9 | 1590 | 5642 | 84 | 83 | 1 | 34 | 58 | 1776 | 0.0148883374689826 | 0.0147110953562566 | 0.000177242112725984 | 0.00602623183268345 | 0.0102800425381071 | 0.314781992201347 | 2036 | 0.360864941510103 |
| 3 | 78702 | 12944540 | 12.94454 | 33 | 34734 | 11 | 766 | 21032 | 120 | 374 | 2 | 22 | 75 | 1603 | 0.00570559147965006 | 0.0177824267782427 | 9.5093191327501e-05 | 0.00104602510460251 | 0.00356599467478129 | 0.076217192848992 | 2196 | 0.104412324077596 |
| 4 | 78703 | 14436159 | 14.436159 | 10 | 92606 | 4 | 1183 | 19873 | 9 | 76 | 0 | 3 | 7 | 565 | 0.000452875761082876 | 0.00382428420469984 | 0 | 0.000150958587027625 | 0.000352236703064459 | 0.0284305338902028 | 660 | 0.0332108891460776 |
| 5 | 78704 | 22503945 | 22.503945 | 21 | 50248 | 7 | 940 | 41709 | 96 | 318 | 2 | 22 | 34 | 2243 | 0.00230166151190391 | 0.00762425375818169 | 4.7951281497998e-05 | 0.000527464096477978 | 0.000815171785465967 | 0.0537773622000048 | 2715 | 0.0650938646335323 |
| 6 | 78705 | 5686651 | 5.686651 | 66 | 11917 | 14 | 1088 | 30532 | 31 | 133 | 0 | 32 | 18 | 924 | 0.00101532818026988 | 0.00435608541857723 | 0 | 0.00104808070221407 | 0.000589545394995415 | 0.0302633302764313 | 1138 | 0.0372723699724879 |
| 7 | 78717 | 33415021 | 33.415021 | 3 | 93305 | 5 | 1018 | 23514 | 10 | 56 | 0 | 1 | 0 | 190 | 0.000425278557455133 | 0.00238155992174875 | 0 | 4.25278557455133e-05 | 0 | 0.00808029259164753 | 257 | 0.0109296589265969 |
| 8 | 78721 | 9588238 | 9.588238 | 32 | 32131 | 16 | 870 | 11178 | 67 | 146 | 0 | 9 | 23 | 394 | 0.00599391662193595 | 0.0130613705492933 | 0 | 0.000805152979066023 | 0.00205761316872428 | 0.0352478081946681 | 639 | 0.0571658615136876 |
| 9 | 78722 | 3919536 | 3.919536 | 19 | 44917 | 8 | 930 | 5973 | 12 | 57 | 0 | 3 | 10 | 265 | 0.00200904068307383 | 0.0095429432446007 | 0 | 0.000502260170768458 | 0.00167420056922819 | 0.0443663150845471 | 347 | 0.0580947597522183 |
| 10 | 78723 | 17979293 | 17.979293 | 29 | 41869 | 10 | 817 | 30999 | 149 | 330 | 4 | 42 | 51 | 1507 | 0.00480660666473112 | 0.0106455046936998 | 0.000129036420529694 | 0.00135488241556179 | 0.00164521436175361 | 0.0486144714345624 | 2083 | 0.0671957159908384 |
| 11 | 78724 | 63858033 | 63.858033 | 38 | 35711 | 8 | 962 | 21677 | 48 | 127 | 0 | 18 | 17 | 327 | 0.00221432855099875 | 0.0058587442911842 | 0 | 0.000830373206624533 | 0.000784241361812059 | 0.015085113253679 | 537 | 0.0247728006642986 |
| 12 | 78726 | 28204228 | 28.204228 | 9 | 66096 | 4 | 1050 | 12482 | 6 | 16 | 0 | 4 | 2 | 176 | 0.000480692196763339 | 0.00128184585803557 | 0 | 0.000320461464508893 | 0.000160230732254446 | 0.0141003044383913 | 204 | 0.0163435346899535 |
| 13 | 78727 | 22190828 | 22.190828 | 11 | 65687 | 6 | 1050 | 28461 | 22 | 78 | 3 | 9 | 5 | 415 | 0.000772987597062647 | 0.00274059238958575 | 0.000105407399599452 | 0.000316222198798356 | 0.00017567899933242 | 0.0145813569445908 | 532 | 0.0186922455289695 |
| 14 | 78728 | 21004795 | 21.004795 | 14 | 47405 | 6 | 901 | 20939 | 0 | 2 | 0 | 0 | 0 | 6 | 0 | 9.5515545154974e-05 | 0 | 0 | 0 | 0.000286546635464922 | 8 | 0.000382062180619896 |
| 15 | 78729 | 23786144 | 23.786144 | 8 | 57358 | 7 | 1008 | 28228 | 22 | 78 | 0 | 4 | 8 | 357 | 0.000779368003400879 | 0.00276321383023948 | 0 | 0.000141703273345614 | 0.000283406546691229 | 0.0126470171460961 | 469 | 0.0166147087997733 |
| 16 | 78730 | 37840281 | 37.840281 | 4 | 119573 | 3 | 1106 | 8312 | 3 | 8 | 0 | 2 | 0 | 38 | 0.000360923965351299 | 0.000962463907603465 | 0 | 0.000240615976900866 | 0 | 0.00457170356111646 | 51 | 0.00613570741097209 |
| 17 | 78731 | 22412156 | 22.412156 | 9 | 78265 | 4 | 1016 | 24716 | 12 | 83 | 0 | 7 | 4 | 421 | 0.000485515455575336 | 0.00335814856772941 | 0 | 0.000283217349085613 | 0.000161838485191779 | 0.0170335005664347 | 527 | 0.0213222204240168 |
| 18 | 78732 | 34465142 | 34.465142 | 3 | 127726 | 5 | 1688 | 14307 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0.000209687565527364 | 3 | 0.000209687565527364 |
| 19 | 78735 | 53215463 | 53.215463 | 6 | 74571 | 4 | 1122 | 16882 | 11 | 50 | 0 | 2 | 2 | 215 | 0.000651581566165146 | 0.00296173439165976 | 0 | 0.00011846937566639 | 0.00011846937566639 | 0.0127354578841369 | 280 | 0.0165857125932946 |
| 20 | 78739 | 29628564 | 29.628564 | 1 | 126525 | 4 | 2000 | 16911 | 1 | 13 | 0 | 1 | 0 | 118 | 5.91331086275206e-05 | 0.000768730412157767 | 0 | 5.91331086275206e-05 | 0 | 0.00697770681804743 | 133 | 0.00786470344746023 |
| 21 | 78741 | 19660250 | 19.66025 | 40 | 30183 | 9 | 835 | 48246 | 225 | 598 | 1 | 54 | 130 | 2386 | 0.00466359905484392 | 0.0123948099324296 | 2.07271069104174e-05 | 0.00111926377316254 | 0.00269452389835427 | 0.049454877088256 | 3394 | 0.0703478008539568 |
| 22 | 78742 | 14852580 | 14.85258 | 37 | 34076 | 11 | 639 | 901 | 4 | 11 | 0 | 2 | 0 | 29 | 0.00443951165371809 | 0.0122086570477248 | 0 | 0.00221975582685905 | 0 | 0.0321864594894562 | 46 | 0.051054384017758 |
| 23 | 78744 | 55439912 | 55.439912 | 26 | 41056 | 9 | 946 | 43452 | 135 | 407 | 4 | 35 | 51 | 1563 | 0.00310687655343828 | 0.00936665746110651 | 9.20556015833563e-05 | 0.000805486513854368 | 0.00117370892018779 | 0.0359707263186965 | 2195 | 0.0505155113688668 |
| 24 | 78745 | 34600328 | 34.600328 | 16 | 49243 | 7 | 990 | 54917 | 120 | 435 | 1 | 34 | 37 | 1950 | 0.00218511572008668 | 0.0079210444853142 | 1.8209297667389e-05 | 0.000619116120691225 | 0.000673744013693392 | 0.0355081304514085 | 2577 | 0.0469253600888614 |
| 25 | 78746 | 58326014 | 58.326014 | 5 | 125327 | 4 | 1221 | 26939 | 6 | 36 | 0 | 2 | 5 | 741 | 0.000222725416682134 | 0.0013363525000928 | 0 | 7.42418055607112e-05 | 0.000185604513901778 | 0.0275065889602435 | 790 | 0.0293255131964809 |
| 26 | 78748 | 32834705 | 32.834705 | 9 | 65889 | 6 | 1095 | 40290 | 48 | 203 | 2 | 13 | 14 | 1270 | 0.00119136262099777 | 0.00503847108463639 | 4.96401092082403e-05 | 0.000322660709853562 | 0.000347480764457682 | 0.0315214693472326 | 1550 | 0.0384710846363862 |
| 27 | 78749 | 26078902 | 26.078902 | 6 | 80956 | 4 | 1150 | 34391 | 26 | 86 | 2 | 6 | 9 | 689 | 0.000756011747259457 | 0.00250065424093513 | 5.8154749789189e-05 | 0.000174464249367567 | 0.000261696374051351 | 0.0200343113023756 | 818 | 0.0237852926637783 |
| 28 | 78750 | 34718029 | 34.718029 | 7 | 75958 | 6 | 1012 | 27119 | 16 | 72 | 2 | 4 | 7 | 308 | 0.000589992256351635 | 0.00265496515358236 | 7.37490320439544e-05 | 0.000147498064087909 | 0.00025812161215384 | 0.011357350934769 | 409 | 0.0150816770529887 |
| 29 | 78751 | 6211942 | 6.211942 | 26 | 38624 | 9 | 865 | 14340 | 22 | 100 | 0 | 8 | 11 | 785 | 0.00153417015341702 | 0.00697350069735007 | 0 | 0.000557880055788006 | 0.000767085076708508 | 0.054741980474198 | 926 | 0.0645746164574616 |
| 30 | 78752 | 8657144 | 8.657144 | 32 | 33271 | 9 | 752 | 17170 | 101 | 162 | 0 | 23 | 49 | 986 | 0.00588235294117647 | 0.00943506115317414 | 0 | 0.00133954571927781 | 0.00285381479324403 | 0.0574257425742574 | 1321 | 0.0769365171811299 |
| 31 | 78753 | 28417686 | 28.417686 | 26 | 39593 | 9 | 826 | 52384 | 184 | 440 | 4 | 58 | 111 | 3138 | 0.00351252290775809 | 0.00839951130116066 | 7.63591936469151e-05 | 0.00110720830788027 | 0.00211896762370189 | 0.0599037874160049 | 3935 | 0.0751183567501527 |
| 32 | 78754 | 34419093 | 34.419093 | 11 | 53274 | 9 | 969 | 13570 | 21 | 94 | 0 | 1 | 2 | 339 | 0.00154753131908622 | 0.00692704495210022 | 0 | 7.36919675755343e-05 | 0.000147383935151069 | 0.0249815770081061 | 457 | 0.0336772291820192 |
| 33 | 78756 | 4329297 | 4.329297 | 9 | 59685 | 4 | 888 | 8060 | 8 | 76 | 0 | 1 | 3 | 267 | 0.000992555831265509 | 0.00942928039702233 | 0 | 0.000124069478908189 | 0.000372208436724566 | 0.0331265508684863 | 355 | 0.0440446650124069 |
| 34 | 78757 | 12732626 | 12.732626 | 16 | 55156 | 6 | 895 | 22718 | 21 | 189 | 2 | 13 | 15 | 858 | 0.000924377145875517 | 0.00831939431287966 | 8.80359186548112e-05 | 0.000572233471256273 | 0.000660269389911084 | 0.037767409102914 | 1098 | 0.0483317193414913 |
| 35 | 78758 | 24052435 | 24.052435 | 24 | 41792 | 10 | 898 | 45105 | 155 | 412 | 0 | 36 | 79 | 2144 | 0.00343642611683849 | 0.00913424232346747 | 0 | 0.000798137678749584 | 0.00175146879503381 | 0.047533532867753 | 2826 | 0.0626538077818424 |
| 36 | 78759 | 36065378 | 36.065378 | 7 | 65672 | 7 | 962 | 39850 | 31 | 156 | 1 | 9 | 15 | 1345 | 0.000777917189460477 | 0.00391468005018821 | 2.50941028858218e-05 | 0.000225846925972396 | 0.000376411543287328 | 0.0337515683814304 | 1557 | 0.0390715181932246 |
From here-- with our .csv file of data, we are ready to put the multilinear regression model to work.
The process of setting up the multilinear regression model on the above data table:
I collected datasets for zipcodes in Austin showing the economic indicators mentioned above for each zipcode (the median income, median rent, and percentage of residents in poverty for 36 Austin, Texas zipcodes). I then cross-referenced these zipcodes with a dataset of about 40,000 crimes that occured in Austin in a particular year. I excluded all zipcodes except those for which I had data for both economic indicators and crimes. I then counted up crimes per category (6 categories total, after similfying category names: Assault, Burglary, Robbery, Theft, Homicide, and Rape), per zipcode. With these two datasets showing economic & crime data for particular zipdoes, we are able to produce an equation showing the degree of confidence with which we can predict rates of crime based on the chosen economic indicators.
The results:
According to coefficient of determination for the various models, we can say that about 70%-80% of the variability in these crimes—Assault, Burglary, and Robbery (for the zip codes examined) can be explained by the variability in the selected economic indicators. That's a pretty strong connection which means that these three types of crimes can be relatively well explained based on these three economic indicators (income, rent, and % of population below poverty)! Based on this study, the other types of crimes examined (homicide and rape) cannot be reliably predicted based on economic indicators– this means they're less determined by economic health of a neighborhood, and more by other unknown/non-analyzed factors.
The ultimate purpose of the project was to create a statistical model from the "training" dataset – i.e. a model that explains the data – and then to test the "test" dataset upon the training model, to check how well the model can be used to predict crime rates based on the economic factors studied.
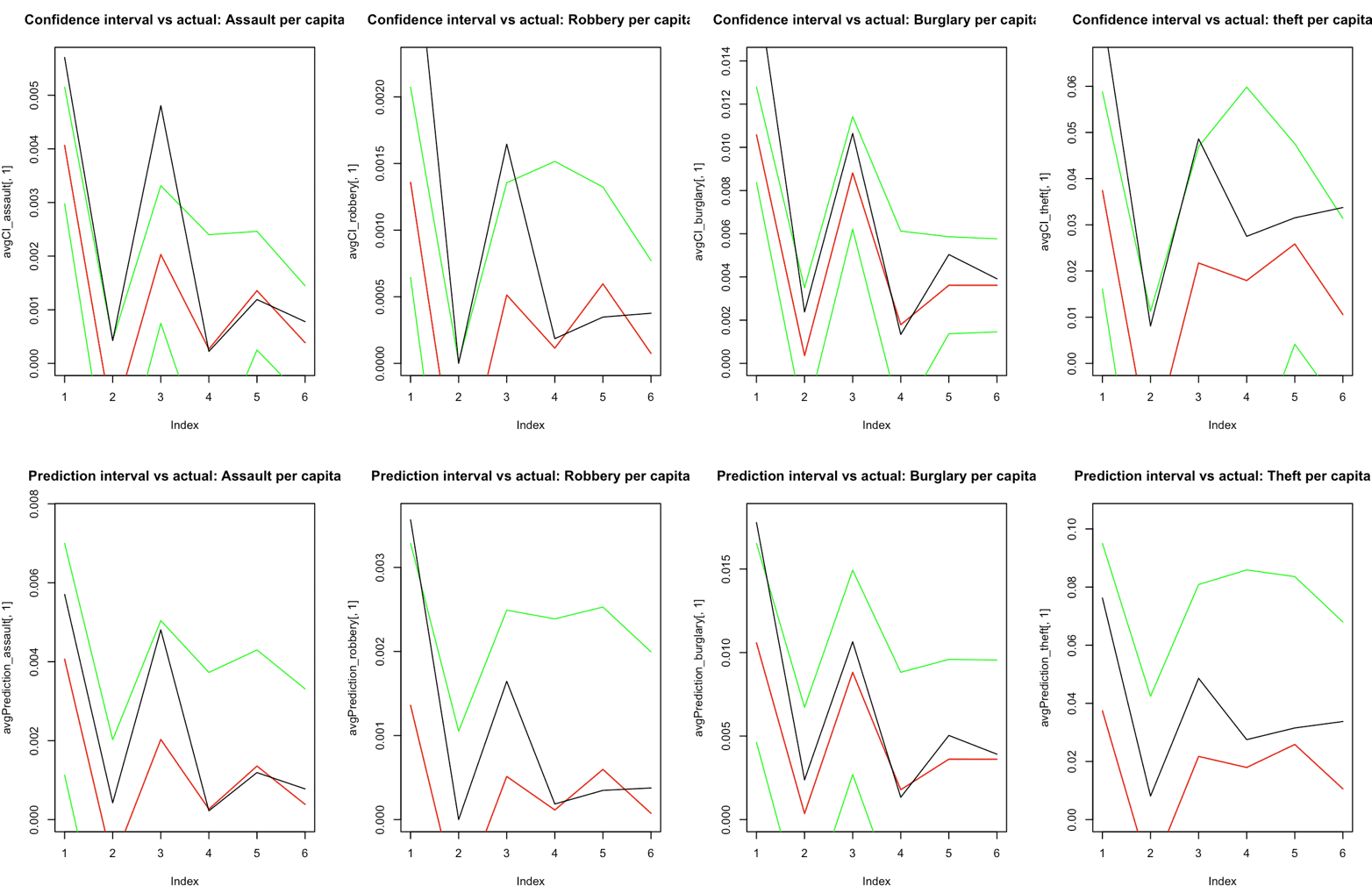
In the statistical charts-- the colorful lines at the top of this page-- we can visualize how well the model predicts crime based on the economic factor inputs from the training dataset. The green lines show the boundaries of a 95% confidence interval (we can be "95% certain" that this interval contains the true mean of the population, which we use the data in the test group to simulate a sample of.), with the redline being the predicted average. The black line represents the actual test data used. As you can see, the green lines capture the majority of the datapoints from the test data, showing that this model (using economic data to explain crimes) does quite a good job of some of these predicting specific crimes (assault, robbery, and especially burglary).
I programmed the project for my two other teammates, who provided guidance, feedback, and ideation, and the final script can be viewed here.
Why do I enjoy statistical analysis?
I enjoy statistical analysis because it is a creative, fun, puzzle-solving way of thinking which allows us to explain the world through data in meaningful, measurable ways.
Throughout this particular statistics course ("Advanced Statistical Methods"), I noticed my thought processes changing. I noticed this especially while working on my statistics project, and for me, I think I really changed between the day I walked into the class, and the day class ended. I realized then that I had began to think more analytically and from a more data-driven, input-output, and equation-based perspective. Crafting equations from data is solving a puzzle– a puzzle where you can produce real and fascinating answers from apparently unrelated datasets! It's quite fun once you get into it!
In addition to changing the way you think, and having fun analyzing a real life puzzle... practicing statistics via scripting will improve your programming abilities! Learning R really helped me become a better programmer because before I could start playing with data, I spent plenty of time learning R's data types and data structures, which was useful when it came time to produce an analysis project and is applicable to programming.
I really like statistics in general for the contribution that the multivariate analysis makes when analyzing any kind of ideas, really. It is quite handy for empirically analyzing all sorts of ideas: whether business decisions, scientific & engineering projects, economic theories, or policy arguments. Being able to formulate an equation or model based on data is a skill in its own right. One of my favorite data visualizations is the "choropleth map", i.e. heatmap.
Here's a choropleth map of Assault frequency for zipcodes in Austin, TX (data is annual assaults reported in 2014).
